伴隨算算子

如果用
< Aχ,χ>/<χ,χ> =>λ1(χ1^h)χ1 / (χ1^h)χ1
直接用Aχ=λχ
也可以把範圍表現出來 這樣寫反而覺得有點不習慣
還是他是想表示χ不為eigenvector也可以表現出其範圍



可以正交對角化是因為A^h=A嗎?





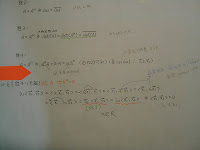
感覺這解法跟normal差不多耶
只差在normal沒有<χ,(A^h)χ>=<χ,Aχ> 這段
感覺上直接用 <χ,(A^h)χ>=<χ,λ(bar)χ>=λ<χ,Aχ>好像比較快
還是因為沒有證出normal所以不可以這樣用

關於伴隨算子還是有些問題
< T(χ),χ>=<χ,T*(χ)>
完全不用任何條件嗎?
因為有看到一個[T*] β=([T] β)^h
上面寫 β基底是orthnormal
是說如果寫成矩陣必須要是用orthnormal才可以用=<χ,(A^h)χ>
這邊我有點搞混了
希望能幫忙釐清一下


不知道有沒有記錯
老師說要把domain縮到球長度為1的球上 才能求極值
不過就算不把domain縮小 仍然可以根據rayleigh principle求出對大值最小值吧?
只是不知道eignevector吧?


順便問一個判定正定方法
像這種寫成cross tern的多項式 調整成A=A^h 其實多項式的結構是沒有改變的
可是有些直接丟一個矩陣
然後問判斷正定的方法
為什麼可以直接調整成Hermitian?
然後利用△去判斷
矩陣結構整個跟原來不一樣
這樣就不是原來的矩陣了@@
這邊我覺得很奇怪 想知道原因
雖說定理是在Hermitian之下才能使用
但是其實全部矩陣都可以調整成Hermitian的樣子啊?
(也是啦...不然有的可以判斷有的不能判斷很奇怪)
可是我還是覺得怪怪的orz


以上懇請大家解惑囉~ 謝謝